visitors.

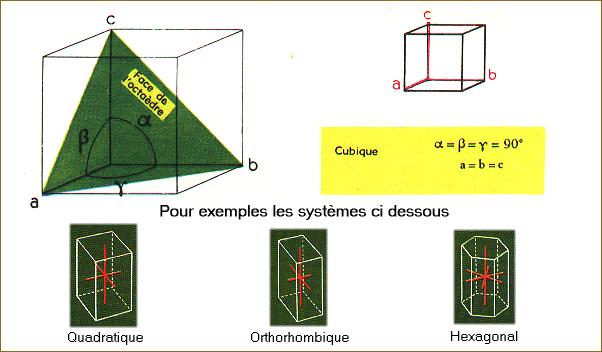
LES SEPT SYSTEMES CRISTALLINS

R J HAUY
le père de la cristallographie / crystallography's father

• En 1781 l'abbé René Just Haüy se trouvant chez un ami collectionneur de minéraux, examinait avec attention un morceau de "spath d'Islande" (variété de calcite incolore et transparente) quand il s'aperçut en le posant sur un texte imprimé que celui ci se voyait dédoublé, surpris par ce phénomène (la double réfraction) il en laissa tomber le morceau de calcite. Il constata que celui ci se brisait en petits morceaux parfaitement parallépipédiques de forme rigoureusement identiques, les rhomboèdres, il s'agissait en fait du phénomène de clivage.

  One day in 1781 abbot Rene Just Hauy examined a piece of "Iceland Spar" (colorless calcite) with a friend and mineral collector, he was so surprised when he saw (by double refraction) two images of a printed text through the sample that he drop it on the floor. He discovered that calcite sample was broken in several parallelepipedic rhomboedres pieces strictly identical.

• Haüy étudia de manière scientifique ces propriétés et fit paraitre sept ans après un essai concernant sa théorie sur la structure des cristaux. Il était parvenu rationnellement à la conclusion que la régularité des formes extérieures d'un cristal reflète exactement l'arrangement des éléments qui le constituent, ces éléments sont disposés en couches parallèles.

  Hauy scientifically studied theses properties and seven years later published his theory on crystal structure.
  A crystal may be constitued by single elements settled in parallel stratification.

Les deux cristaux ci dessus sont constitués par un empilement régulier de petits cubes qui sont les constituants élémentaires du cristal, exactement comme les rhomboèdres du morceau de spath d'islande. Cette notion de constituant élémentaire définie par R J Haüy sera ultérieurement appelée unité de croissance ou unité de base du modèle atomique cristallin.
Les constituants de base sont disposés sous forme de couches parallèles qui sont en fait des couches de croissance. La croissance d'un cristal se fait donc dans une direction qui forme toujours un angle droit avec la face concernée; de plus, sa surface va diminuer à mesure que le matériau se déposera. Imaginons que la face en cours de croissance constitue la face supérieure d'une pyramide tronquée; plus la pyramide s'élèvera, plus cette face supérieure diminuera, jusqu'à devenir la pointe de la pyramide.

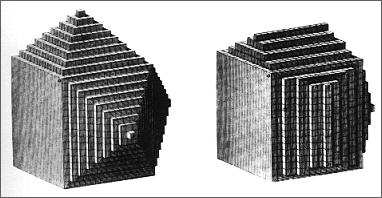
The two crystals reproduced on the above picture are made of little cubes exactly like little abbot Hauy's Iceland Spar rhomboedes. These elementary parts are named growing parts or basic particle of atomic crystal model.
Growing parts are arranged in parallel layers which are in fact growing layers. The crystal growing process is made according to a righ direction of the concerning face of the crystal; in addition to, the growing face surface will decrease during the growing process. For exemple if the growing face if the upper face of a truncated pyramid, these face will be the top of pyramid.

On constate donc qu'à partir de la même particule élémentaire (ci dessus le cube), on obtient selon les minéraux et les processus de croissance des formes de cristaux diverses.

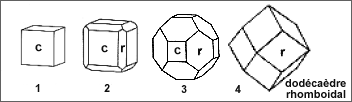
Selon l'exemple I, on passe progressivement d'un cube à un dodécaèdre rhomboidal. According to exemple N° I the cube become gradually rhomboidal dodecaedron.

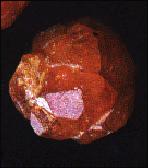Le grenat, qui, occasionnellement forme également des cubes, compose plus fréquemment des dodécaèdres (photo de droite) ou des trisoctaèdres encore appelé trapézoèdre: solide à 24 faces (photo de gauche)

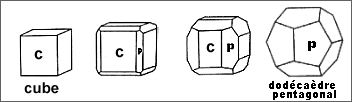
Selon l'exemple II, on passe progressivement d'un cube à un dodécaèdre pentagonal According to exemple II the cube become gradually pentagonal dodecahedron.

La Pyrite qui forme habituellement des cubes parfaits, forme aussi des dodécaèdres pentagonaux... ainsi que d'autres polyèdres. Pyrit that make usually perfect cube, make also pentagonal dodecahedron.

• Les axes de symétrie : Considérons le cube.
  • Si l'on fait passer un axe par le centre de deux faces opposées, on constate en faisant tourner le cube sur cet axe qu'il se retrouve dans une position identique à chaque rotation de 90°. Cet axe correspond donc à une symétrie d'ordre 4, il est encore appelé axe quaternaire. ( fig 1 )
    Le cube possède six faces et donc trois axes quaternaires.
  • Si l'on fait passer un axe par le centre de deux arêtes opposées, en faisant tourner le cube sur cet axe, il se retrouve dans une position identique à chaque rotation de 180° . cet axe correspond à une symétrie d'ordre 2 encore appelé axe binaire. ( fig 2 )
    Le cube possède 12 arêtes et donc six axes binaires.
  • Si l'on fait passer un axe par deux sommets opposés, on constate qu'il faut une rotation de 120° pour retrouver une position identique . Cet axe est donc de symétrie d'ordre 3 et encore appelé axe ternaire. ( fig 3 )
    Le cube possède huit sommets et donc quatre axes ternaires.

• Les centres et les plans de symétrie
  • Deux ou plusieurs axes de symétrie concourants déterminent un plan de symétrie.
  • Le point de concours de plusieurs axes de symétrie ou de plusieurs plans de symétrie est appelé centre de symétrie.

• Les pinacoides / pinacoid: Imaginons l'un des axes étudiés ci dessus ( ici un axe vertical z ) et une face qui lui serait parallèle, isolée dans l'espace. ( fig 4 ci-dessus) Si l'axe est binaire, on obtient par rotation de 180° autour de cet axe une autre face parallèle; on dit que l'ensemble forme ainsi une figure appelée "pinacoide".
  Si l'axe est ternaire, on obtient trois faces décallées de 120° limitées latéralement par leurs intersections et illimitées dans le sens de la hauteur. Cette forme qui ressemble à une boite ouverte aux deux extrémités, constitue en fait un prisme à section triangulaire.
  Le pinacoide tout comme le prisme sont des formes "ouvertes" qui peuvent être limités par deux plans appelés "bases", mais aussi par des bipyramides, des rhomboèdres ... etc qui sont des formes "fermées".

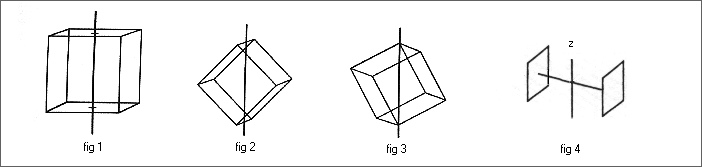
  The pinacoid is composed of only two parallel faces and can be thought of as the top and bottom of a book. ( see fig 4 )
  Pinacoid like prism are "open forms" which may be limited by two plane named "bases", but also by dipyramid, rhombohedron ... etc which are "closed forms"

• Le prisme: est un solide de forme géométrique simple possédant (si il est fermé ) deux bases de même forme parallèles entre elles, et dont les faces latérales sont des parallélogrammes; il est dit "droit" si les faces latérales sont perpendiculaires aux bases (elles sont alors des rectangles ou même des carrés), et "oblique" quant elles sont obliques sur les bases.
  Le prisme cubique utilisé pour la démonstration ci dessus est un prisme droit dont toutes les faces sont carrées.
  Le prisme quadratique est un prisme droit dont les bases sont carrées et les faces latérales rectangulaires, la brique ancienne dont la hauteur et la largeur sont égales, alors que la longueur est différente est en fait un prisme quadratique.
  Le prisme orthorhombique est aussi un prisme droit mais dont les bases et les quatre faces latérales sont des rectangles, la brique actuelle le représente parfaitement.

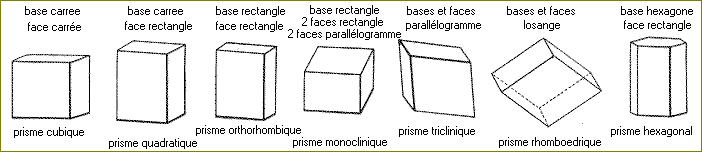
  Le prisme monoclinique est oblique selon une direction, les deux faces latérales inclinées selon la direction sont des parallélogrammes, si l'on reprend le cas de la brique actuelle, les deux bases sont toujours des rectangles ainsi que deux faces, les deux autres faces sont des parallélogrammes. On peut l'obtenir en déformant par exemple l'enveloppe extérieure d'une boite d'allumettes posée à plat par pression du doigt sur l'une des arêtes de la face supérieure.
  Le prisme triclinique est oblique selon deux directions, on peut le représenter comme un prisme monoclinique dont les faces seraient aussi des parallélogrammes.
  Le prisme rhomboédrique possède six faces identiques (comme le cube) mais en forme de losange, on peut le comparer à un cube que l'on aurait écrasé (rhomboèdre obtus) ou au contraire étiré (rhomboèdre aïgu) par deux de ses sommets opposés. C'est aussi un prisme monoclinique dont les bases seraient des losanges et dont les faces latérales seraient des losanges identiques, ou encore un prisme triclinique dont les bases et les faces seraient aussi des losanges identiques.

  Le prisme hexagonal contrairement aux autres prismes dont les bases sont toutes constituées par des quadrilataires, possède deux bases de forme hexagonales, il est parfois considéré comme étant la réunion de trois prismes à bases en forme de triangle équilatéral; ses faces latérales sont rectangulaires.

  Il n'existe en fait que ces sept types différents de prismes qui sont susceptibles d'être empilés sans laisser de vide entre eux, en d'autres termes remplissant exactement l'espace.
  Si un cristal appartient au système orthorhombique (par exemple), cela signifie qu'il suffira d'empiler (comme pour les cubes ci dessus) autant de prismes identiques qu'il le faut pour reconstituer son ensemble.
  Ces sept types de prismes constituent les polyèdres élémentaires des sept systèmes cristallins.

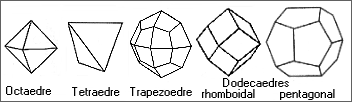
Ci dessous quelques formes fermées simples du système cubique.

L'octaèdre est en fait une bipyramide cubique, les formes fermées simples et les bipyramides se retrouvent parfois entières sous forme de cristaux. Le plus souvent les bipyramides terminent les cristaux prismatiques droits, elles existent donc dans les systèmes cubiques, quadratiques, orthorhombiques et hexagonaux.

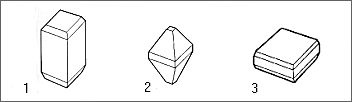
Une bipyramide, un prisme et un pinacoide peuvent aussi se combiner pour former un habitus ( un faciès )

1) prismatique
2) pyramidal
3) tabulaire

comme dans le système tétragonal, ( voir figure ci dessous ); mais aussi comme pour de nombreux cristaux prismatiques droits.

Pour étudier les systèmes cristallins, il est commode de se reporter à leurs axes de référence. Ce sont trois droites imaginaires parallèles aux faces du cristal, le choix des longueurs et des directions de ces axes est en relation avec les longueurs des cotés de l'unité de croissance cristalline. Ces axes sont appelés a,b et c et semblables aux axes cartésiens mais ils sont construits sur des éléments existants c'est à dire les arêtes du cristal; on choisit les trois arêtes qui représentent le mieux la symétrie du système et qui est la plus répandue, par exemple le cube pour le système cubique, le prisme quadratique pour le système quaratique, le prisme hexagonal pour le système hexagonal ...etc
Ces arêtes doivent se joindre pour former un sommet commun, nous avons donc trois axes possédant une origine commune, il reste à translater l'ensemble de manière à ce que l'origine coïncide avec le centre du cristal, on obtient alors les axes cristallographiques ou axes de référence; les angles entre les axes sont appelés alpha, beta et gamma.
Dans le système le plus symétrique ( le système cubique ), ils sont tous trois égaux et font entre eux des angles droits, dans le système le moins symétrique ( le système triclinique ), aucun des angles n'est un angle droit et les axes tout comme les angles d'ailleurs peuvent être inégaux entre-eux.

• Le système Cubique.
• Le système Tétragonal.
• Le système Hexagonal.
• Le système Rhomboédrique.
• Le système Orthorhombique.
• Le système Monoclinique.
• Le système Triclinique.

Last Revised on Dec 2005 / Dernière mise à jour: Dec 2005

• Retour à la page principale / Return to the main page Gemmes et minéraux
• Retour à la page cristallographique Cristaux et cristallographie